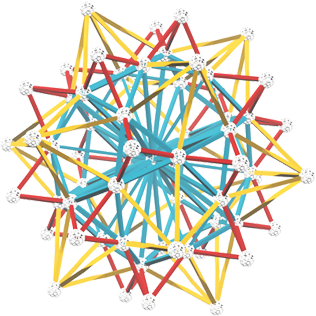
阿基米德多面体的星状化
阿基米德多面体星状化，是以阿基米德多面体的每个面为底面，外接棱锥形成的图形。这种几何体的形状非常奇特，像是由许多星形组成的立体图案。

阿基米德多面体-截半立方体
阿基米德立体是指由正多边形面构成、且每个顶点的局部结构相同的凸多面体，共有13种。当前图形由 8 个三角形和 6 个正方形组成。

阿基米德多面体-截角八面体
阿基米德立体是指由正多边形面构成、且每个顶点的局部结构相同的凸多面体，共有13种。当前图形由 6 个正方形和 8 个六边形组成。

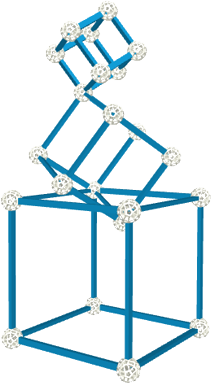
正方体叠拼
这是一个由大、中、小三个正方体叠拼的一个艺术作品。他们边长之间比例符合黄金分割率。

阿基米德多面体-截角立方体
阿基米德立体是指由正多边形面构成、且每个顶点的局部结构相同的凸多面体，共有13种。当前图形由 8 个三角形和 6 个 八边形组成。

超立方体
超立方体也称为四维立方体，它是由 8个三维正方体所组成的四维图形，这个模型所展示的是超立方体在三维的投影。

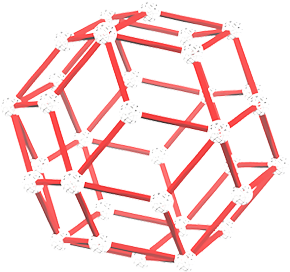
菱形三十面体
菱形三十面体有30个相等的菱形的面和12个顶点。这个菱形恰好是黄金菱形，也就是说，它对角线的比例为黄金分割比。这个立体的截半恰好是 Zometool 小球所对应的多面体。

正十二面体与正二十面体对偶
将正十二面体的每个面上的中心点连接起来，得到一个正二十面体的顶点。正二十面体的每个面的中心点连接起来，得到一个正十二面体的顶点。这些多面互为对偶，将一个面连到对方的顶点，展现了自然中的神秘连接。

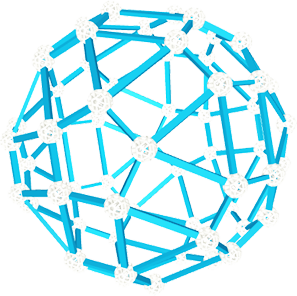
Zometool球
Zometool球包含62个面，其中有30个长方形面，20个三角形面，12个五边形面。长方形的长与三角形边长一致，长方形的宽与五边形边长一致。这个图形是由阿基米德多面体通过调整棱长变化而成，结合了多种形状，完美塑造了棱长的变化与组合之美。

谢尔宾斯基的四面体分形
分形是一种具有自相似性的图形，它的一部分看起来像是整个图形的缩小版。
谢尔宾斯基的四面体分形是一种基于谢尔宾斯基三角形的三维分形结构。这种分形通过不断地对一个四面体（也称作三角锥）进行递归分割和去除某些部分来生成复杂的几何图案。

120胞体
120胞体是一种存在于四维空间的形状，这意味着它很难想象或绘制。 这里拼搭的结构是它在三维空间的投影。它就像是十二面体在四维空间中的版本。科学家研究120胞体，以更深入地了解不同维度中形状的工作方式。

600胞体
600胞体是一种存在于四维空间中的几何体，是四维空间中的正多胞体之一，也是胞体数最多的正多胞体，由600个正四面体和120个顶点组成。它与120胞体互为对偶。这里拼出的图案是600胞体在三维空间中的投影，120个四维顶点投影之后，有一部分重合，最后剩下75个不同的三维顶点，所以这里用到了75个小球。

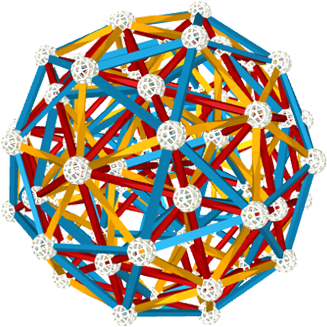
开普勒模型
开普勒宇宙模型是由德国天文学家约翰内斯·开普勒在16世纪末提出的一种宇宙观。他认为正四面体、正六面体、正八面体、正十二面体和正二十面体，这五个多面体是宇宙的基本结构，后被证明是错误的。但是确实就只有这五种正多面体。后来数学家康威提出了一种将所有正多面体嵌套起来的方式，并证明这是最紧密的嵌套方式。

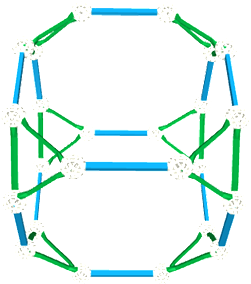
绿线模型
通过正十二面体中的5个正四面体相互穿插构成的结构，塑造了立体的交互与和谐。

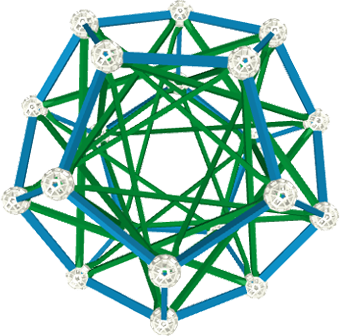
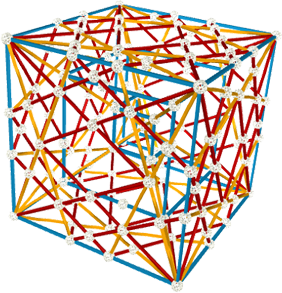
镶面堆叠超立方体
这是一个以超立方体为基础的堆叠造型，在最外层的面进行了镶面装饰，整个造型结构稳定并呈现出一个视觉效果极佳的立方体。

正方体的截面
正方体的截面可以是三角形，四边形，或者六边形。本模型展示了截面刚好为正六边形的情况。

桁架梁桥
桁架桥梁是一种采用钢桁架结构的桥梁，具有强度高、重量轻、施工方便等优势。它的发展历史可以追溯到19世纪，如布鲁克林大桥等都采用了桁架结构。目前，桁架桥梁已被广泛应用于公路、铁路等交通建设领域。像中国的南京长江大桥就是桁架结构设计的标志性建筑。

高塔
高塔结构是高度超过300米的建筑物，主要采用混凝土或钢结构，成为城市的地标建筑。自艾菲尔铁塔建成以来，高塔结构经历了多个阶段，如现代主义、超现代主义。它具有视觉冲击力和经济效益，著名的塔建筑如广州塔，纽约自由塔等。

蜜蜂窝结构
蜜蜂的六边形蜂巢是一个完美的几何结构，它们展示了如何用最少的材料构造出最稳定的结构。

三维立方体在平面上的投影表现为两个嵌套正方形，它们的顶点两两相连。