穿越六大数学文明
解说词

在这里,各类几何物体和超维模型带你去探索无限延展的几何星海。你将乘坐克莱因飞船,开始一段穿越六大数学文明的冒险之旅:
N-S流体文明:居民像魔法师一样控制水流。
向量基地:可以随意缩放万物,无论缩小到原子️,还是放大到宇宙。
混沌星系:通过微小变化,利用“蝴蝶效应”创造奇迹。
庞加莱拓扑星:任意改变物体形状,建筑和地形都可以随心变形。
无穷∞世界:科技可以分解一切再重组,循环无尽。
穿越神秘的拓扑迷宫,再到不可预知的概率深渊,最后,飞船带你抵达数学大统一世界。数学奥秘从“一”延展到无穷,再从无穷回归到“一”,让你体验这场奇幻的数学冒险之旅!

高维之旅
出发啦!克莱因船在这次数学探险中,发现许多神秘的数学文明。

在这趟探险中,我们会发现一个巨大的挑战,那就是“无穷”的概念!
不管是无限大的宇宙,还是微观世界里那些看不见的极小粒子,无穷都贯穿在所有数学规则之中。
但是,数学家们还在寻找一个更大的秘密,那就是能解释所有数学规律的理论!
想象一下,如果我们能找到一个能把“1到∞”所有复杂问题都总结起来的答案,那会是什么样子?
能够把无穷大的宇宙和无穷小的微观世界连在一起,成为一个完整的故事。
这就是我们要寻找的大统一数学理论!
第一站:N-S流体文明

科学原理
纳维-斯托克斯方程描述了流体(如水和空气)的运动,包括河流、海洋的流动以及天气中的气流,但解决复杂的湍流现象仍是数学难题。
N-S方程

就是描述水流如何流动的魔法公式!
这些方程虽然看起来复杂,但很酷哦!
水流的行为受很多因素影响:速度、粘度(就是水的粘稠程度),还有周围的物体,像小石头。科学家和工程师会用到N-S方程,预测水流的行为,帮助他们设计船只或控制洪水,确保安全,保护大家。
N-S方程让我们了解,水流中的每一个细微变化,就像在探寻自然的秘密,真是数学与自然的美妙结合!
第二站:向量基地

科学原理
向量的重要特性是它的“可缩放性”,向量可以被放大或缩小,而其方向和比例保持不变,例如矢量图可以无限放大或缩小而不会失去清晰度。
第三站:混沌星系

科学原理
混沌理论中,蝴蝶效应描述了初始条件的微小变化可能导致系统中巨大、难以预测的后果。一个蝴蝶扇动翅膀,可能在遥远的地方引发一场风暴。
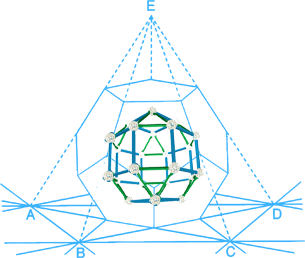
第四站:庞加莱拓扑星
科学原理
庞加莱猜想证明了三维空间中的封闭曲面像一个球体,可以通过拓扑变换转化为其他形状。
第五站:无穷∞世界
无论敌人多么强大和神秘,他们都可以先对其微分,分解敌人结构,找到弱点;然后通过积分精准打击弱点。这使得无穷文明几乎无敌。
除了战争,无穷文明还会通过微积分将低维文明“积分”成知识和技术的养分,不断吸收其他文明的智慧,进化并扩展自己的科技边界。

科学原理
微积分通过微分和积分,可以解析微小变化并累积结果。无穷文明利用这些数学原理累积数据,将其彻底击败。无穷序列则使他们的科技可以无限扩展,不断进化。
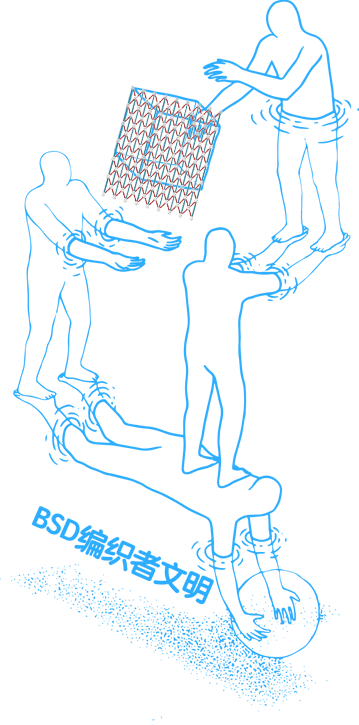
第六站:BSD编织者文明
在编织星空文明中,居民们用一张看不见的网相互连接成一个“整体大脑”,星星、树木、河流都通过这张“数学网”连接起来。编织者们能够利用这张网预测气候、找到资源,甚至研究更复杂的宇宙结构,试图破解BSD猜想中揭示出的数论和代数之间的深奥联系。

克莱因船在数学的高维世界探险过程中,见过无数的数学文明。 历经六大文明的探险之后,克莱因船终于抵达了数学大统一之路。

但是,要真正理解这个宇宙,我们还需要一个统一所有数学规律的理论——让从1到∞的所有复杂问题,最终汇聚成一个简单的答案,也就是从∞到1。这呼应了数学家克莱因提出的愿景:将数学分支连接在一起形成一个完整的数学宇宙。