无穷小的世界

 解说词

有令人震撼的超大数，也有趋近于零的无穷小∂。
一条曲线分成无数小段，每一段接近直线。
从无穷小看到微小变化，这就是微积分的魔法钥匙！
了解无穷小，才能明白行星的运动。理解无穷小，才能推演流体的变化。
无穷小的分割和累积，能看清宏观宇宙的复杂。无穷小是数学逻辑，可以推理出自然界的秩序。
通过掌控无穷小∂，才能理解无穷大。

推理力打卡暗号：
从无穷小中👀无限大的逻辑

无穷小的魔法尺

探索了越来越大的数字世界，现在让我们进入越来越小的神秘世界吧！
想象一下你有一把神奇的魔尺，它能测量任何大小的东西。

这把魔尺能变成米尺（1米）
量一量好朋友的身高。

变成毫米尺（10^-3米）
测量蚂蚁的触角长度。

变成微米尺（10^-6米）
测量细菌的直径。

变成飞米尺（10^-15米）
测量原子核的尺寸。

继续缩小到量子尺（10^-35米），我们遇到了普朗克长度。普朗克长度是我们目前知道的最小长度。

难道你能小到和我一样吗？

如果有一把“无穷小”的尺子，比普朗克长度还小。
它可以变得超级超级小，就像魔法一样，帮助我们测量所有的东西。
但小到消失不见了，小到无限接近0，还能测量吗？
那岂不无穷多个长度为0的点=长度为1的线段？
无穷小这种无限缩小的特性，导致了一些令人费解的现象和悖论。

令人抓狂的无穷小

无穷小非常重要，如果没有无穷小，我们就很难精确地描述过程。
如果没有无穷小，我们就不知道底层的逻辑是什么样子。
早在很久以前，古人也在思考无穷小的奥秘。

穷竭法

为了揭开无穷小神秘的面纱，数学家们薅秃了头发，探索并思考各种关于无穷的问题。
其中一个就是：如何计算曲线围成的面积？

古希腊的安提丰提出了一个极具影响力的思路：穷竭法，来计算圆形的面积。
先作一圆内接正方形，将边数加倍，得内接8边形；再加倍，得16边形……
无限重复这个过程，圆的面积就无限接近于正多边形面积。

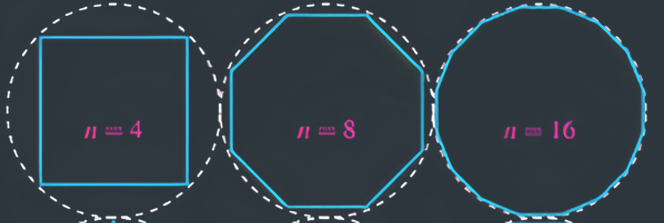
穷竭法为计算圆面积圆周率等问题提供了方向。

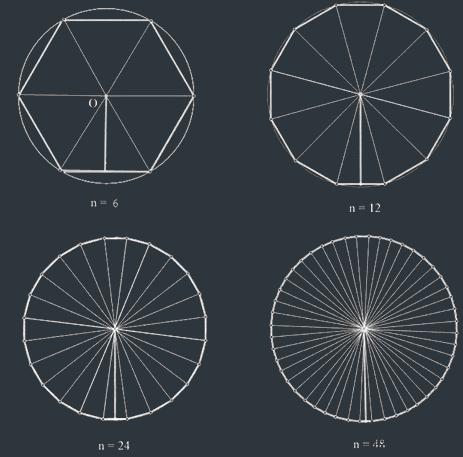
魏晋时期，刘徽在注释《九章算术》时提出了“割圆术”。
他将圆分割成多边形，分割得越细，多边形的面积就和圆面积越来越接近，这是我国早期的极限思想。
刘徽通过"割圆术"将π的值精确到了3.1416。

阿基米德通过将圆分割成内接正多边形，计算圆外接多边形和内接多边形的周长来估计圆周率，最后得出π的值在223/71到22/7之间。

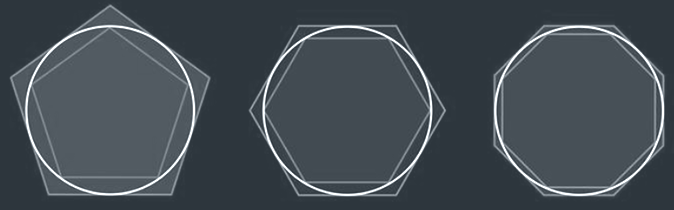
阿基米德极大地推广了穷竭法，他不仅用此方法研究了圆，还研究了许多其它的曲线。
比如阿基米德用三角形求出下图的弓形面积。

阿基米德将抛物线与线段之间的面积分割为无数个三角形。
每一个三角形都以同样的方式内接于一个抛物线弓形，比如蓝色三角形被整个弓形面积所内接，绿色三角形则内接于蓝色三角形占据后剩下面积的弓形中。
这些方法体现了“无限分割”的极限思想，初步窥探到微积分的冰山一角！

极限
想象一把很长的尺子，你想找一个肉眼看不见的小刻度。用放大镜放大后，你能看到更小的刻度，但永远无法看到最小的那个。
在数学中，这个过程叫“极限”。我们不断接近一个值却永远达不到。
极限是微积分中的基本概念，帮助我们理解变化率和累积量。它让我们处理不精确但可接近的问题，即使不能完全达到目标，但可以通过努力无限接近它！

神奇的以直代曲

学会了穷竭法，但我们依然没有获得计算任意曲线围成的面积的灵丹妙药。因为计算起来太麻烦了，穷竭法需要为每种形状单独设计分割策略，这在实际操作中既费时又费力。
而且我们从小就学了各种求面积的公式，什么长方形、三角形、圆、梯形等等，学一种新图形就有一个新的面积公式，可是，世界上有无数种图形啊，难道要记无数种公式么？
请求出此刻内心的一块阴影面积！
就不能把曲线掰直，变成直线再计算吗？我们是不是需要想办法把曲线用直线表示出来呢？
就像一根麻绳，我们把麻绳捋直了再测量长度，问题是不是就简单了很多？

假设我们将一个圆分成8等分，并将这些等分重新排列，形成一个近似平行四边形的图形。
然后，继续将圆分成16、32、64等分，随着分割的不断细化，边线逐渐变得平滑，最终接近于长方形。

当我们继续分割下去，32等分，64等分，随着切割的无限细分，接近无穷小，最后就能拼接成一个长方形。

所以捋直曲线的奥义就是无限切割，直到接近无穷小！每个小线段就是直线。

想象一下，小朋友们，我们站在地球上，此刻我们脚下的地面就是地球一个无穷小的点，此刻我们坚信，脚下的地面是平的，即使我们知道地球是个球体。

现在我们再回头看看圆形，如果将一个圆用竖条进行无限的划分，那么每个竖条可看成一个矩形，把这些矩形的细长短条的面积相加，就是圆的面积！

在数学中，无穷小是微积分的基础。它允许我们把一个令人头疼的问题分解成无穷小的碎片，打碎重组为更简单、更熟悉的事物！
这就是微积分的经典-以直代曲！