莱布尼茨的楼梯

 解说词

莱布尼茨曾遇到了一个有趣挑战，假设一个人正在爬一段高达99层且不太规则的楼梯，每层楼梯高度都不一样。
第一层高 $\frac{1}{1x2}$ ，第二层高 $\frac{1}{2x3}$ ，第三层高 $\frac{1}{3x4}$ ，最后一层高 $\frac{1}{99x100}$ ......
如果攀登者想测量从楼梯底部到顶部的垂直高度，他如何才能做到呢？

无穷级数的挑战

这个挑战其实是莱布尼茨的老师惠更斯出的一个难题。
惠更斯：出道题考考你！如何求解下面这个无穷级数的和？

$\frac{1}{1x2}$ + $\frac{1}{2x3}$ + $\frac{1}{3x4}$ + $\frac{1}{\mathrm{n}\mathrm{(n+1)}}$ + ... = $?$

我们将每一项都看做一层楼梯的高度，那么这个99层高的莱布尼茨楼梯即变为求解下面算式之和：

$S=$ $\frac{1}{1x2}$ + $\frac{1}{2x3}$ + $\frac{1}{3x4}$ + $\frac{1}{\mathrm{n}\mathrm{(n+1)}}$ + ... + $\frac{1}{99x100}$

当然，你可以把每个台阶的垂直高度全部加起来，如果你一层一层的累加，它就是一个冗长的计算过程，虽然你总能加完这99层。

但这如果变成 层呢？！

难道真的要一层楼梯一层楼梯加起来吗？想想真是个可怕的事情！

看看莱布尼茨是怎么解决这个问题的。莱布尼茨开始研究楼梯的高度变化，发现这些楼层每一项都可以改写为连续差之和的形式，这在计算中引发大规模抵消现象。

$S=$ $(\frac{1}{1}-\frac{1}{2})$ + $(\frac{1}{2}-\frac{1}{3})$ + $(\frac{1}{3}-\frac{1}{4})$ + ... + $(\frac{1}{98}-\frac{1}{99})$ + $(\frac{1}{99}-\frac{1}{100})$
$=1-\frac{1}{100}=\frac{99}{100}$

so easy！就是这么简单！

复杂的连续相加一下子变成了简洁的首尾相减，如果图中的攀登者有一个高度计，他就可以用楼梯顶部的高度减去楼梯底部的高度来解决这个问题，不管楼梯有多么不规则，这个方法都行之有效。就避免了一层层累加这么繁琐的事情。
一个全新的世界打开了，分割和累积里面隐藏着惊天的秘密，莱布尼茨顿悟了。
之后莱布尼茨把这个思路推广到不规则的求和问题，最终发现了牛顿莱布尼茨公式！

${\int }_a^b$ $f\left(x\right)dx=F(\left()b\right)-F\left(a\right)$

微积分就像一把神奇的钥匙，能够打开科学世界的大门，帮助我们理解周围世界的运作方式。

麦克斯韦方程组
在电磁学领域，麦克斯韦方程组描述了电场和磁场如何相互作用，让电子设备得以工作。

薛定谔的方程
在量子力学中，薛定谔的方程揭示了微观粒子的神秘行为。

几何学求体积
在几何学中，微积分帮助我们测量各种形状的体积。

$V={\int \int \int }_{x^2+y^2}^{4-x^2-y^2}dzdydx$

傅里叶变换
而在信号处理和图像分析等领域，傅里叶变换则发挥着至关重要的作用。

谁是微积分之父

在数学的历史长河中，微积分的诞生标志着一个革命性的转折点。尽管关于谁是微积分之父的争论一直存在，但无可争议的是，艾萨克·牛顿和戈特弗里德·威廉·莱布尼茨共同奠定了微积分的基础。

牛顿：运动的瞬间变化
牛顿爵士从物理学的角度出发，将微积分应用于描述物体运动的瞬时变化率，如速度和加速度。他的工作为后来的物理学和工程学提供了强大的工具。

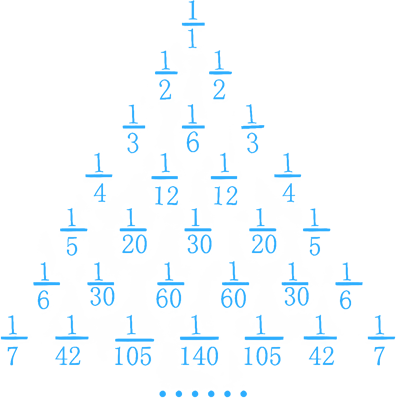
数学和平大使
为了纪念牛顿和莱布尼茨这两位伟大的数学家，小朋友可以化身“数学和平大使”，与他们的立牌握手，以此象征他们之间的和解与友谊！